머신러닝 - 정규화

cs231n 수업에서 보충하기 위해 

코드잇을 이용하는 거라 

포스팅이 이어지지는 않음

 

 

머신러닝 모델이 정확한 예측을 하지 못하는 경우를

해결하기 위해

"편향"과 "분산"이라는 개념이 필요

 

편향

사람의 키를 이용해서 몸무게를 예측하고 싶다고 하자

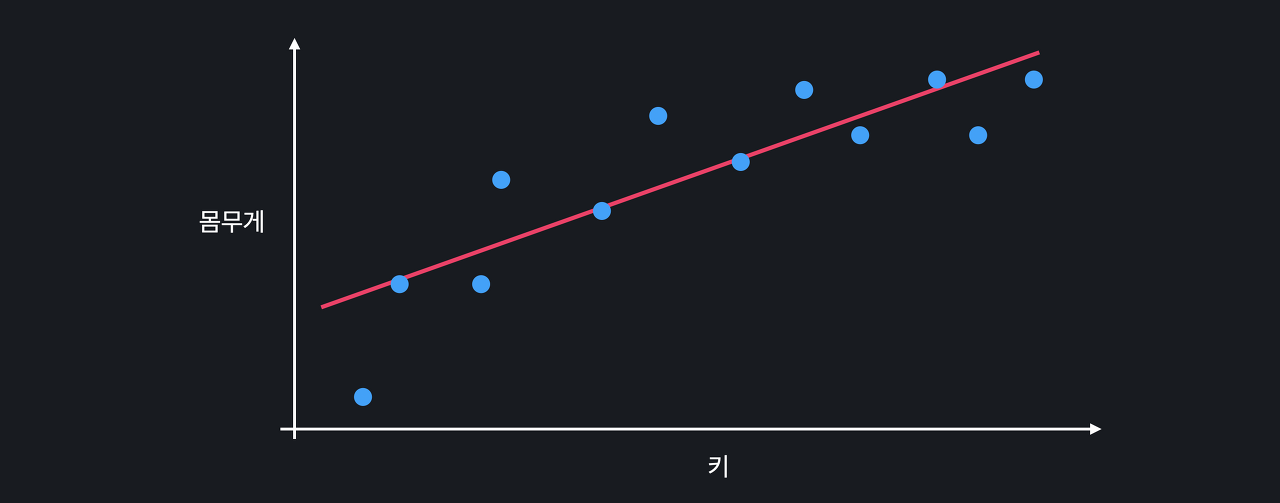
선형 회귀를 사용

위의 선이 과연 몸무게와

키의 관계를 잘 표현하고 있을까?

 

일정 키부터는 몸무게가 잘 안 늘어남

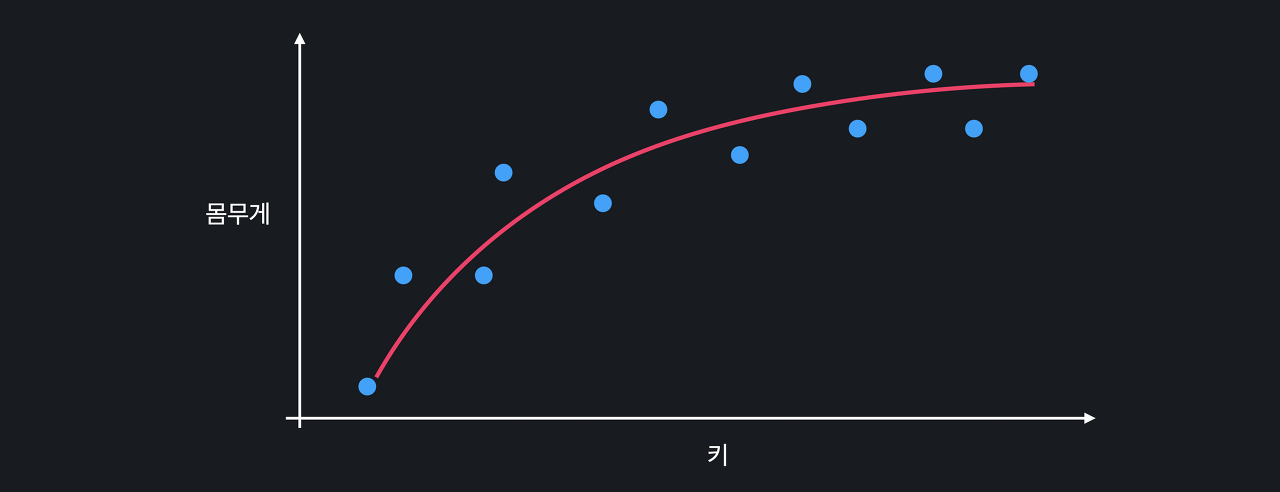
따라서 아래와 같은 곡선이 데이터를 더 정확하게 표현 가능

 

 처음에 본 직선 모델의 문제는 모델이 너무 간단해서

아무리 학습을 해도 위와 같은 곡선 관계를 나타내지 못함

 

즉, 모델에 한계가 있음

 모델이 너무 간단해서

데이터의 관계를 잘 학습하지 못하는 경우

모델의 편향, 영어로는 bias가 높다고 함

 

편향이 작은 모델을 살펴볼까요?

이번에는 높은 차항의 회귀를 사용해서,

위와 같은 관계를 학습했다고 하자

이 복잡한 곡선은 training 데이터에 거의 완벽히 맞춰져 있음

 

 모델의 복잡도를 늘려서

training 데이터의 관계를 잘 학습할 수 있도록 한 것

따라서 이 모델은 편향이 낮은 모델

 

 

그러면 편향이 낮은 모델은 항상 편향이 높은 모델보다 좋을까?

NO

분산

위에서 봤던 직선 모델과

복잡한 곡선 모델을 이용해서

처음 보는 test 데이터의 몸무게를 예측해 본다고 하자

왼쪽은 training 데이터, 오른쪽은 test 데이터입니다.

평균 제곱 오차를 사용해서 모델의 성능을 평가할 거임

 

먼저 복잡한 곡선 모델부터 보자

이 모델은 training 데이터에 대해서는 거의 완벽한 성능을 보이지만

test 데이터에 대해서는 상당히 안 좋은 성능을 보임

 

하지만, 모델의 성능은 

test 데이터의 성능을 의미하는 거임

아무리 training 데이터를 잘 예측하더라도,

test 데이터를 잘 예측하지 못하면 의미없음

 

 

모델이 오히려 너무 복잡해서 문제가 생김

 

모델이 training 데이터를 가지고 학습할 때

키와 몸무게의 관계를 배우기보다는

아예 데이터 자체를 외워버리기 때문에

처음 보는 데이터 셋에 모델을 적용해 보면 성능이 아주 떨어지는 것

 

 

데이터 셋 별로 모델이 얼마나

일관된 성능을 보여주는지를

분산, 영어로는 variance라고 함

 

다양한 데이터 셋 간에

성능 차이가 많이 나면 분산이 높다고 하고,

성능이 비슷하면 분산이 낮다고 함

 

복잡한 곡선 모델은

데이터 셋마다 성능 차이가 많이 나니까

분산이 높은 것임

 

 

그럼 직선 모델을 보자

training set을 사용했을 때랑,

test set을 사용했을 때 성능에 큰 차이가 없음

 

 

다양한 데이터 셋을 사용해도 일관된 성능을 보임

따라서 직선 모델은 분산이 작음

 

정리

 

1) 편향

편향이 높은 머신 러닝 모델은

너무 간단해서 주어진 데이터의 관계를 잘 학습하지 못하고

 

편향이 낮은 모델은

주어진 데이터의 관계를 아주 잘 학습함

 

첫 번째로 본 직선 모델은 편향이 높고,

두 번째로 본 복잡한 곡선 모델은 편향이 낮습니다.

 

 

 

2) 분산

 

분산은 다양한 테스트 데이터가 주어졌을 때

모델의 성능이 얼마나 일관적으로 나오는지를 의미

 

직선 모델은

어떤 데이터 셋에 적용해도

성능이 비슷하게 나오지만,

 

 

복잡한 곡선 모델은

데이터 셋에 따라 성능의 편차가 굉장히 크기 때문에

 

 

직선 모델은 분산이 작고,

곡선 모델은 분산이 큽니다.

 

편향과 분산

편향과 분산보다 조금 더 직관적인 용어를 사용해서 다시 한번 정리하자

 

이 직선 모델은 복잡도가 너무 떨어지기 때문에

키와 몸무게의 곡선 관계를 학습할 수 없음

 

 그 대신 모델이 간단하기 때문에

어떤 데이터가 주어지든 일관된 성능을 보임

 

위 모델은 편향이 높고, 분산이 낮은 모델임

 

 

이런 경우 모델이 과소적합,

영어로는 underfit 

 

모델이 training 데이터에 과소적합 됐다라는 말

 

반면 이 복잡한 곡선 모델은 training 데이터에 너무 잘 맞는 게 문제

 

training 데이터의 패턴을 학습하는 게 아니라

데이터 자체를 외워버리기 때문에

training 데이터에 대한 성능은 아주 높지만,

처음 보는 test 데이터에 대한 성능은 많이 떨어짐

 

 

편향이 낮고, 분산이 높은 모델

이런 경우는 모델이 과적합, 영어로는 overfit 됐다고 함

 

모델이 training 데이터에 과적합 되었다라고 말함

 

모델이 training 데이터의 관계를 잘 나타내지 못하면 과소적합,

관계를 지나치게 잘 나타내면 과적합. 좀 더 기억하지 쉽죠?

편향-분산 트레이드오프 (Bias-Variance Tradeoff)

 일반적으로 편향과 분산은 하나가 줄어들수록 다른 하나는 늘어나는 관계

 

둘 중 하나를 줄이기 위해서는

다른 하나를 포기해야 된다는 말

>> 그렇기 때문에 이 관계를 편향-분산 트레이드오프라고 부름

 

 

편향-분산 트레이드오프 문제는

머신 러닝 프로그램들의 성능과 밀접한 관계가 있기 때문에

편향과 분산, 다르게는 과소적합과 과적합의 적당한 밸런스를 찾아내는 게 중요

 

 

이런 딱 적당한 곡선을 찾아야 한다는 것

 

 

 

 

 

 

 

정규화

 

‘과적합 문제 직접 보기’ 영상에서 봤듯이 복잡한 모델을 그대로 학습시키면 과적합이 되기 마련임

 

‘정규화’라는 기법은 학습 과정에서 모델이 과적합 되는 것을 예방해 줌

 

위와 같은 학습 데이터를 이용해서 다항 회귀를 하는 경우를 생각해보자

모델이 과적합 돼서 아래와 같은 복잡한 다항 함수가 나왔다고 가정

 

 

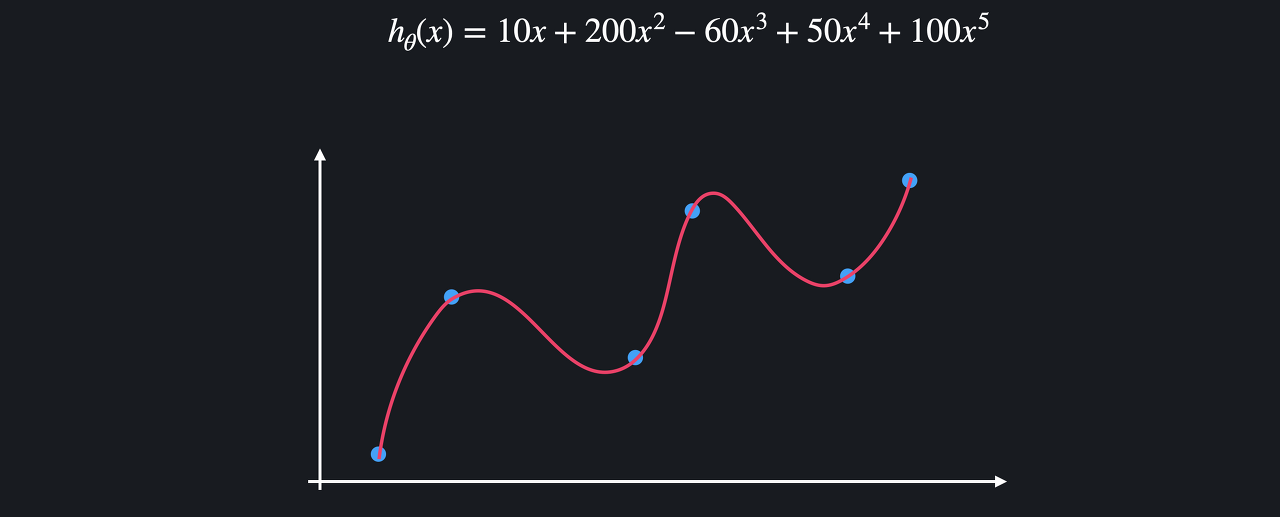
과적합된 함수는 보통 위아래로 엄청 왔다 갔다 한다는 특징 존재

 

많은 굴곡을 이용해서

함수가 training 데이터를 최대한 많이 통과하도록 함

 

함수가 이렇게 급격하게 변화한다는 건 함수의 계수,

즉, 가설 함수의 θ 값들이 굉장히 크다는 뜻

 

정규화는 모델을 학습시킬 때 θ 값들이 너무 커지는 것을 방지해 줌 

θ 값들이 너무 커지는 걸 방지하면

training 데이터에 대한 오차는 조금 커질 수 있어도,

위아래로 변동이 엄청 심하던 가설 함수를 좀 더 완만하게 만들 수 있음

 

 

 

이런 함수는 여러 데이터 셋에 대해

더 일관된 성능을 보이기 때문에 과적합을 막을 수 있는 것

 

 

 

L1, L2 정규화 차이점

 

 

 

 

L1과 L2 정규화의 차이점

L1과 L2의 차이점은 아래와 같습니다:

L1 정규화는

여러 θ값들을 0으로 만들어 줌

모델에 중요하지 않다고 생각되는 속성들을 아예 없애준다

 

L2 정규화는

 θ값들을 0으로 만들기보다는 조금씩 줄여 줌

모델에 사용되는 속성들을 L1처럼 없애지는 않는 것

 

아마 그림으로 보면 더 쉽게 이해되실 텐데요: